The Political Economy of Participatory Economics - by Michael Albert and Robin Hahnel
Nonetheless, there is one more step to make our argument complete. All theorists
feel their theories are consistent and comprehensive. But often, of course,
theorists are wrong. They present elegant, internally consistent arguments that
seem accurate and comprehensive, but nonetheless lead to predictions at odds
with reality. For example, we have argued elsewhere that traditional theorists
have produced elegant and consistent but not so comprehensive and accurate arguments
concerning the predictable attributes of capitalist and centrally planned economies.
So how can a theorist justify confidence in a set of theoretical results? What can others do to become more confident of our results or, alternatively, demonstrate their inadequacies? Of course it is possible to keep thinking about the results, reviewing the logic behind them, trying to discover inconsistencies or unwarranted assumptions. But it is also possible, at least in scientific disciplines, to conduct experiments. A good theoretical, scientific argument therefore includes indications of how to carry out experiments that might test predicted results.
So we need to specify some plausible, economic experiments. However, social environments are for obvious reasons notoriously hard to experiment with. The easiest "experiments" to implement are a variety of computer simulations in which various features of the system and assumptions about actors' behaviors can be altered to see how outcomes change. More problematic is implementing a whole "trial" participatory economy. While we feel there is little to lose from doing so, others might not share our low opinion of existing economies. But it is also possible to imagine establishing a kind of parallel participatory economy-or allocation system, in any event-alongside an existing market or centrally planned system. Without disrupting the functioning of the existing economy, differences between decisions reached via the two procedures could then be compared.
In this chapter we briefly describe a methodology for undertaking these "experiments." No new analyses or predictions regarding the behavior of participatory economic structures are presented and the material is chiefly for economists who want to undertake the experiments themselves. Since each of the "experiments" could usefully employ tools that actors in a real participatory economy would employ to keep track of proposals and results, and since describing these tools will also provide a review of how a real participatory economy should work, we start with this task.Tracking a Participatory Economy
To generate a participatory plan, each consumer proposes the amount of each
good she or he wishes to consume and the anticipated changes in her or his personal
or material relations that will result. Each consumption unit proposes inputs
and outputs equal to the sum of its members' proposals plus any collective goods
or services desired. Larger consumption federations propose a summation of all
member units' lists plus collective consumption.
Each production council chooses inputs and outputs including "technology," work hours, social relations, and labor intensities. Each industry sums its members' proposals. The whole economy's production is a summation of all its industries. From the production side there emerges a "net supply" of goods to meet a net "consumption demand" arising from consumer preferences.
Information Variables for a Participatory Economy
In chapter 5 we developed a mathematical formalism sufficient
to demonstrate a series of propositions about a participatory economic model.
We could arguably employ the same formalism for computer simulations that we
would then use to determine the mean and variance of the number of iterations
required to reach a feasible plan in a range of cases. Likewise, a variant of
the mathematical formalism from the previous chapter might be usable for certain
indicative calculations by actors in a real participatory economy. However,
we indicated that there were some important differences between real participatory
economics and its idealized model. Since we want any simulation we undertake
to tell us about the realistic system and not our continuous mathematical model,
we want the experiment's variables to be flexible enough to continually incorporate
greater detail about the discrete behavior of a real system. Practically, we
also want the simulation's variables to be suitable for programmers to incorporate
as data types. And the same holds for a formalism that could be employed in
a parallel participatory planning experiment within an existing economy. Here
too, we do not want to use the kind of continuous variables that proved useful
for technical proofs. Instead, we need a formalism suited for storage and retrieval
of large amounts of discrete quantitative and qualitative data in an economy's
computers, and useful to real producers and consumers who do not solve differential
equations to make their decisions.
For all these reasons we begin by elaborating a new formalism suited to use in developing computer simulations and to continual refinement and enrichment in the course of experimentation.
We write the vector Cj, to represent consumer j's consumption input. To refer to consumption output, we
write ![]() where
the bar tells us we are talking about outputs. Likewise, each production input
vector will have entries corresponding to labor, machines, resources, and intermediate
goods so Pj represents production inputs of unit j and
where
the bar tells us we are talking about outputs. Likewise, each production input
vector will have entries corresponding to labor, machines, resources, and intermediate
goods so Pj represents production inputs of unit j and ![]() represents its outputs. In other words:
represents its outputs. In other words:
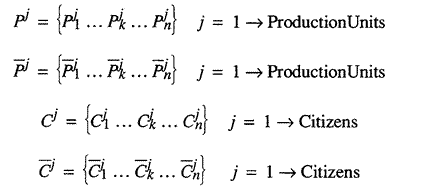
where n is the total number of all inputs and outputs.
Elaborating the new "language," a list is a sequence where each entry can be
numbers, words, vectors, or even another list describing qualitative characteristics.
For example, we could associate a special descriptive list with each workplace
and with every input and output consumption actor. Vectors help actors assess
quantities. Lists help actors assess qualities.
Finally, for every workplace there is a unit production matrix that, when multiplied by an input vector yields the unit's output vector. For convenience we can make all unit production matrices n by n, recognizing that many entries will be zero. Clearly, there is no technical impediment to communicating and manipulating information in these forms since computer techniques already allow efficient manipulation of vectors, matrices, and lists.
Manipulating Information
Each of our economy's industries has an input and output vector and a production
matrix formed by aggregating the input and output vectors and production matrices
of its members. Each consumer prepares a personal consumption input and output
vector and list. Consumer units propose "summations" of their members' personal
choices plus collective choices. This proceeds upward, until the whole economy
has overall input and output consumption vectors summing all units' members'
consumption plus all collective consumption.
For the first iteration, each worker proposes not only what she or he will contribute, but inputs and outputs for the whole plant. To get an indicative plant proposal out of all these worker proposals, we sum and then divide by the number of workers. This average is the best available estimate since at this stage no single viable plan better represents a summary of all workers' preferences. In later rounds input and output vectors for production units emerge directly as individuals no longer make separate proposals.
The industry matrix represents how all its units together act on input vectors.
The societal matrix does the same for all industries composing the whole economy.
Summing unit or industry production matrices involves taking a weighted average
where the "weighing factor" is the relative volume of output in units. In a
sense, each firm's production matrix is a "recipe" telling what ingredients
will yield unit outputs of the "dinner" it is trying to prepare. By multiplying
these "recipes" by any quantity of ingredients we can see what size meal will
result. Alternatively, knowing the size of our dinner party, we can multiply
the size meal we seek by the inverse of the production matrix to determine the
ingredients needed. To sum the efforts of all the different cooks in all the
different firms in an industry we simply add them together, taking account of
the relative scale of operation of each to get an overall production matrix.
We already know that for the first two rounds, depending on iteration rules
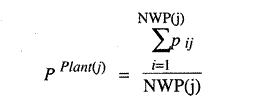
where PPlant(j)
is the production input vector of the jth plant in the industry, NWP(j)
is the number of workers in the plant, and pij is the ith worker's proposal
for inputs for plant j.
For all subsequent rounds, units submit single proposals rather than proposals of each worker, and so for all rounds and the final plan
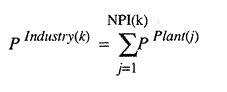
where PIndustry(k)
is the input vector for the kth industry in the economy and NPI(k)
is the number of plants in industry k, and
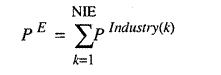
where PE
is the input vector for the whole economy and NIE is just the number
of industries in the economy, and, of course, similar results hold for outputs.
Considering the problem of summing lists, it would be inefficient to repeat
a particular qualitative description just because each actor in a unit repeats
it. Neither would it make sense to append conflicting statements in a growing
jumble. Instead, if five consumers each have different qualitative descriptions
under the entry referring to milk consumption, the unit's overall description
should summarize all five in a short expression. Similarly, the same aggregating/summarizing
process should occur for transition from units to neighborhood, neighborhood
to ward, ward to county, and so on. We should remember, however, that all actors
will have access not only to aggregated summary lists prepared by iteration
facilitation boards, but to each unit's and individual's full formulation as
well.
Functional Relationships
Suppose we look at values for a projected year. First we know that the unit,
industry, or economy production input vector times the unit, industry, or economy
production matrix will yield the unit, industry, or economy production output
vector.
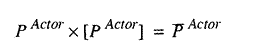
Second, for a plan to be feasible, the economy's production output vector must
equal the total final consumption input vector plus the intermediate inputs
of all the industries plus any planned slack.

The superscript "E" means that our vectors refer to the whole economy. SLE
is just our vector of all the [SL]ack pre-planned as a hedge against
unforeseen changes in taste or productivity. Moreover, since equality of vectors
only holds when each entry is equal, the above expression is shorthand for n
equations, one for each vector entry. Here we can see that total supply for
the economy is simply the output of the economy's production units. Total demand
for the economy, on the other hand, is the sum of slack, production inputs,
and consumer and consumer council inputs.
How does each unit and actor implement desires? What determines production matrices? What determines what the list of attributes of economic processes will be and how much each actor and collective unit will consume?
In assessing these and related questions, economists traditionally take consumer preferences, work force knowledge and skills, and technical options as independent variables determined outside the economy, and "derive" the values of what are called endogenous variables-inputs, outputs, and prices-under a particular institutional arrangement. Although this traditional approach is called a "general equilibrium" theory to emphasize that all factors mutually determine one another, in fact it treats certain factors as essentially determined outside the economy. In particular it ignores the fact that the institutional arrangements affect the "independent" variables, as we have pointed out. In contrast, while we recognize that extraeconomic forces influence economic attributes, we make all economic institutions, norms, knowledge, preferences, prices, and quantities endogenous to the model.
Simulation Methodology
A simulation mimics how a participatory economy would operate under various
assumptions about behavior and choices of planning rules. To use our "language"
to track supply and demand in a simulation, we need iteration rules for economic
behavior as well as working assumptions about how planning might affect people's
tastes and behaviors.
For example, suppose one wants to test the hypothesis that some attribute, Z, necessarily characterizes participatory planning. One would need to demonstrate that the trajectory of development from first proposal to agreed plan to enacted plan necessarily enforces attribute Z under the full range of anticipated circumstances. Likewise, by using simulations one could investigate implications of changes in behavioral rules on outcomes. For example, one might study relations between the number of iterations allowed, the rules for each iteration, the speed with which actors settle on a plan, and the attributes the plan will have-over some range of assumed behaviors.
Alternatively, one could use simulations to research the effect of iteration workers on the plan's likely character, or the effect of planning collective consumption or industrial "investment" before rather than concurrently with personal consumption. Or we could compare the time it takes to go from random first round proposals to a settled plan, to the time it takes using first round proposals based closely on last year's final outcomes. Or we could test the effect of intransigence on the part of some range of participants. Or one could even try to determine under what behavioral assumptions a participatory economy would yield the same material outcomes that markets or central planning would produce.
But how would one actually undertake any of these studies? So far we have indicated only how to track part of what is going on. How can tracking hypothetical data facilitate analyses of what real economies would be like?
This done, using behavioral assumptions and stipulating starting conditions, one could, with a sufficiently powerful computer and effective program, simulate a hypothetical economy to yield diverse insights about likely outcomes for different rules, behaviors, initial conditions, and so on.1. We need to track more variables, including prices, loans, and budgets.
2. We must determine how to simulate behavior in ways that realistically summarize consumers' and producers' diverse and altering preferences so we have something to track.
3. We must determine how to incorporate the effects of iteration rules.
Incorporating Prices and Budgets
Suppose we define every item, i, used in our economy (including labor) as having an indicative price pi , so we can write a price vector
![]()
Any good or service embodies many other goods and services in its production, so that if we take one unit of any good or service "G,"
![]()
where G is a vector each of whose entries are the amount of the relevant item directly employed in producing one unit of G.
Suppose all society's actors settle on input and output vectors thereby establishing a plan. We can easily investigate the economy's techniques to determine and regularly update G for all goods so that once our planning process socially sets relations of production and inputs and outputs, indicative prices can be mechanically calculated by solving a system of linear equations. In short, social planning sets the relations between goods which in turn establish indicative prices, so that once we solve for these:
1. To find the socially valued worth of each consumption bundle we multiply the amounts of each good received by its price and sum.
2. To find the socially valued worth of the inputs and outputs of any plant, we multiply the amounts of these by their prices and sum.
Using V as a value operator to return "value" equal to a sum of prices times items
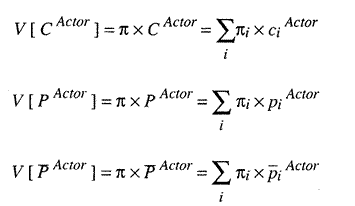
We now easily define an actor's "loan" as the difference between the value of what the actor planned to receive and what the social average was after accounting for special circumstances that lead others to allow actors to go above or below average.
What about budgets? On the producer side, units assess their efforts and make proposals while respecting their projected industry per unit average output and their per resource productivity as guides to ensuring that their "social effectivity" is sufficient.
On the consumer side, each consumer ultimately settles on a bundle of consumption goods. The value of these, added to the per capita value of the consumer's public goods consumption, constitutes the total value of the consumer's consumption. Neglecting special excuses, loans, and/or debts, this must equal the societal average which serves, therefore, as a consumer budget.
What is the societal average consumption and therefore the budget constraint operating for each consumer? Clearly it is the value of total consumption for the economy divided by the total number of consumers.
![]()
Simulation Actors
Consumers request goods and services in light of their needs and desires knowing
that others will not approve unreasonable requests and that they will have to
play an equitable role in producing whatever is to be consumed. Producers respond
to consumer requests in light of their own needs and growing awareness of social
circumstances. They balance their desires to work less and in more favorable
circumstances against their own and other consumers' desires to consume more.
How can we simulate the behavior of hundreds of millions of consumers and workers?
One simplification would be to use a scaled-down model including only a limited number of consumers and producers and a few intermediate and final goods. This approach would allow us to get a feel for the interaction at the micro scale. Another, more robust, option would be to truncate the choices of countless consumers into summary variables indicating total consumer demand for each of the available final consumer goods. This approach would give us better insight into the global trajectories of participatory planning. It also offers the option of establishing a kind of "game" format in which an individual, acting as a consumer or producer, interacts with the global simulation as one actor in the whole process.
To perform a small-scale simulation, we would let a few production units and consumption councils operate in the manner of real actors giving them hypothetical technologies and preferences and having a computer simulate their behavior as well as that of facilitation boards, and the like. In this way, tests with a given set of planning rules under different stipulations of technologies, preferences, and initial indicative prices would reveal how a particular system responds to different choices by the limited number of actors. Alternatively, one could keep the "economic environment" of technology and preferences constant and vary the planning rules to get an indication of the effects of different rule choices. The disadvantage of this kind of simulation is obviously that a real economy has tens of millions of participants, so that one might reasonably doubt that such simulation results are valid indicators of real results.
To pursue the more global approach requires some way of summarizing large numbers
of producers' and consumers' behaviors. While the laws of probability and properties
of the normal distribution can aid us considerably in doing this, there is a
characteristic of production that requires a tactical compromise. In large-scale
simulations we can incorporate differences in consumers' preferences by treating
the demand for final goods as distributed normally around some mean. But differences
in workers' preferences over work options cannot be treated so simply because
factors other than their normally distributed personal preferences come into
play in their choices, specifically, the special (and non-normally distributed)
characteristics of production units. To do a simulation that tracks the behavior
of every unit in each industry in the economy in light of its own particular
characteristics would strain the capabilities of any available computer and
no probabilistic shortcuts can fully circumvent this difficulty. But modeling
industries rather than firms within industries is manageable, and using this
approach we only lose details at the firm level, such as differences among firms
due to unequal technologies. We of course still need a procedure to allow each
industry to arrive at new proposals in each iteration, but we ought to be able
to develop one in a way that acceptably approximates the range of possible outcomes
that could arise from actually summing individual changes in each of the industry's
firms. Thus, if we are content to simulate the behavior of industries rather
than firms within industries, we can pursue large-scale simulation experiments
as described below.
We require a way of simulating the sum of all producers' and consumers' behaviors so as to work with net supply and demand of industries on the one hand, and with net consumer demand for final consumption goods on the other. Ideally, the simulation would help identify the bounds that behavior would have to fall within for the system to operate desirably under some range of planning rules. So can we really expect to sensibly go from hundreds of millions of consumers or millions of consumers' councils to total consumer demand for each good without incorporating any individual choices?
The task is similar to trying to simulate the behavior of gases in enclosed containers. No one can track the positions and velocities of all the molecules. Even with a supercomputer, this micro approach would be fruitless. But if we ask what proportion of the molecules will be where with this or that velocity we can understand and simulate important macro properties like pressure and temperature without confronting the behavior of each individual gas molecule.
Analogously, in studying hypothetical participatory economies we cannot possibly
simulate the individual choices of millions of individual production units and
hundreds of millions of individual consumers. For production units, as noted
above, we forgo details of individual units and track industry behavior instead.
What about consumption?
The obvious choice is to pay attention only to consumers' councils or federations. Better still is to track only total demand for each final good. The idea is to deduce qualities of the trajectory of collective behavior in light of iteration rules, the size of the economy, and plausible assumptions about the range of consumers' behaviors and how these sum to total supply and demand. Regarding consumption, to assess total demand we only need to know that some number of people will choose one thing, and another number of people will choose another, ignoring who will choose what. By bypassing each individual's particular behaviors we only lose information regarding the exigencies of individual interaction with the system. Does the individual get bogged down, inevitably become irritated Does the size of consumer units play a role in the rate of the whole process? Do geographic distributions matter? Some of these possibilities can be assessed, however, by constructing a means for a real individual or group of individuals to join in the simulation process at a real time terminal connected with the unfolding simulation.
Returning to the general problem of summarizing total consumption without incorporating individual actor's behaviors, we can reasonably assume that consumers' preferences will form a normal curve whose main characteristics are completely determined by two parameters, mean and standard deviation, where the maximum number of respondents always occurs at the mean and varies directly with the total number of respondents and inversely with the standard deviation. Knowing these gross attributes can so simplify the simulation that we can do it for any number of hypothetical consumers.
Suppose we track the milk totals all citizens request in the first iteration of a year's plan. We can say nothing definitive about any one person's choice but we can plausibly assume that the distribution of the choices of all actors will fall on a normal curve. If we assume this is true for all goods, plausible conclusions can be reached. But even this hypothesis could be checked by also undertaking simulations assuming other probability distributions.
Incorporating Actual Behavior
Having settled on industries and the whole population of consumers as our unit
actors, from iteration to iteration, for each good the simulation must incorporate
algorithms for generating new indicators for total supply (production output)
and total demand (production input plus consumer demand plus slack) in light
of assumptions about the interaction between consumer and producer behavior,
the prior status of each good, available qualitative information, and the like.
One can then program the simulation to calculate product status for each new
iteration up to the final plan.
To get total supply in each iteration we will need to incorporate a rule for how each industry goes from one proposal to the next in light of possible iteration rules, the prior status of each good, and the producers' preferences for work versus leisure. A sensible rule would include a component for moving toward (or away) from the prior iteration's consumer demand (or the iteration-board projected consumer demand for the current iteration) plus a component for moving toward or away from the prior iteration's (or the current projected) total production requirement (averaged over units). To build in a spectrum of unpredictability reflecting diverse and changing producer preferences as well as the effect of diverse iteration rules that would appear in a real society, we can imagine programming into our algorithm a degree of weighted random choice that would be correlated with supply and demand conditions and with allocation rules. In this way we can reasonably test for a whole range of conceivable industry preferences.
For example, we might employ a rule that for any industry the proposal in a current iteration will reduce the discrepancy between supply and demand in the prior iteration for the industry's good by a random multiplier between -.25 (which would increase by 25% of the discrepancy) and .5 (which would reduce by 50% of the discrepancy) with a bias introduced by always adding some particular fraction, say dG to the random number picked by the computer where the range of dG would increase or decrease in tune with supply and demand conditions, iteration rules, some attribute of the particular industry, and so on. We could then test for the effect of different definitions of dG reflecting different possible producer response characteristics as well as different initial ranges of proposal alterations. To refine the system still further, we could put in proportionality factors to account for the different values of the output of different industries thereby keeping the drift in industry proposals from one iteration to the next within some range regarding their impact on overall consumption budgets. Naturally, as a byproduct of dealing with producer proposals for output we automatically handle producer inputs as these are directly calculable from outputs by way of production matrices and, in this light, a further refinement in the algorithm would incorporate attention to the impact of underor oversupply of its own input components in each unit's tendency to decrease or increase its production proposal. It should be clear that while we have not explicitly incorporated production preference functions for individual workers, we have indicated a means to simulate the full range of conceivable behavior patterns that possible workplace characteristics and workers' preferences could induce.
This said, however, we still have the problem of simulating consumer demand. First we can plot any consumer demand distribution to generate a list of ordered pairs, (x,y) where the x-entry is a desired amount that a consumer could propose as her or his demand, and the yentry is the total number of consumers proposing that amount. In this light we can usefully write consumer demand distributions for a particular good in a particular iteration, I, as CI(G), where this operator returns lists of ordered pairs. The "I" superscript will take on (1) the number value of the iteration if we are talking about an iteration distribution, (2) the value "p" if we are talking about the plan agreed to by the planning process, or (3) the value "f" if we are talking about the year's [f]inal outcomes as they are actually enacted.
In a real economy we would of course get our ordered pairs for any iteration's consumer demand distribution from summing all the participatory planning consumer input vectors, thereby incorporating precise actor by actor information. Yet, in our global simulation, even without knowing or predicting every consumer's own unique input vector, we can still simulate total consumer demand for each good by using distributions to represent gross characteristics of taste, much as we used a statistical range of production iteration choices with flexible parameters and built-in biases to simulate the effects of diverse producer preferences and plant characteristics on industry production proposals. We therefore skip the enumeration of vectors for every actor and instead jump directly to approximate expressions for the entire ensemble of actors.
Define for any consumer demand distribution for iteration "I" the total demand for the good G, D(G), to equal the sum of the number of people demanding a certain amount of G times the amount for all such ordered pairs in that consumer demand distribution.
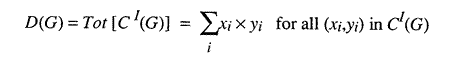
Tot operates on a consumer demand distribution for any good to give the total demand for that good. Each of the terms added is just the number of actors times the amount they want to consume. We can now define [ST]atus of the good G in the iteration I as the difference between the total supply offered and the total demand and slack desired for that good in that iteration. Tot and ST are operators that return numbers, not vectors or lists. Remembering that total supply is just production output and total demand is consumer demand plus producer input demand plus slack:
![]()
If we define the net supply of any good G, SI(G), as the total producer output of G minus the total producer input of G, or the amount of G coming from production and available for slack or consumer demand, we can write the simpler equation:
![]()
Given all this, and assuming that it can converge, the participatory planning process can be summarized in the following succinct fashion. For any good G, the net supply distribution follows the trajectory
![]()
and likewise for demand, slack, and status distributions with suitable changes in notation.
The problem is to discern what range of planning rules and what types of consumer and producer behavior will allow the status trajectory of each good to move toward zero in an acceptable number of iterations.
Within our simulation methodology we have already indicated the main ideas for establishing algorithms for arriving at each new iteration's producer inputs and outputs for any G given the prior iteration's results. This establishes net supply. Since slack is socially chosen, its level is at the disposal of the simulator. Only consumer demand remains.
In each iteration all consumers receive a facilitation board projection for total societal and average per capita consumption of each good and for estimated average consumption bundles and unit by unit production averages. Since we know how to track these variables, what we need to know to describe the macro-trajectory of our economy's net supply, its consumer demand distributions, and its slack requirements from iteration to iteration until the model settles on a plan, is how to characterize the effects of preferences, planning rules, current divergences, and choices about budget levels on changes in consumption distributions from iteration to iteration.
Consumer Demand
Parameters distinguishing any particular economy depend on the economy's number of actors, number of products, number and structure of industries, and technologies.
The first iteration proposals presented by all producers and consumers sum to determine net supply and total consumer demand proposals which, coupled with preferences about slack, determine status relations for each good. Since in our modeling we bypass individual preferences, the aim of our earlier discussions of individual behavior was to: (1) reveal the underlying dynamics of macro relations, (2) demonstrate a notation to allow facilitation board manipulations and public reporting in a real economy, and (3) further clarify the source of indicative prices.
Now, however, to pursue a macro approach we must focus on consumer distributions and the changing statuses of simulated goods, not on individual actor's activities.
We start by assuming that for every good, G, there is a first round C1(G) characterized by a mean,
m{C1(G)} and standard deviation s{C1(G)} for each good.
We also write for any good that its distribution's facilitation board projected
average for an iteration-just the average amount demanded per consumer - is
Proj[CI(G)] and
similarly or net supply. We also define d{CI(G)}
and d{SI(G)}
to be the "proportionality factor" between the real mean of the demand
and the netsupply of good G and their before-the-fact projected averages.
![]()
So that, if
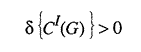
the projected average is less than the actual registered average and if
![]()
the projected average is more than the actual registered average, And, likewise
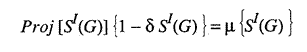
So that if

the projected average is more than the actual registered average and if
![]()
the projected average is less than the actual registered average.
Then, extending and simplifying this notation, the hypothetical average consumer requests a total amount of any good (I DELTAC) x (the projected average demand for that good), forinulated with a plus sign to reflect the likelihood that the average consumer will have a higher estimate of economic growth than facilitation workers. Likewise, the average producer proposes to supply a total amount of any good (I - 6S) x (the projected average supply for that good), reflecting the likelihood of producer optimism.
It is important at this point to note that while unique indicative prices are calculable for any balanced plan, no such prices are calculable for early iteration proposals that are not yet balanced. To use our value function during iterations we must use prices that derive indirectly from facilitation board workers' updated estimates of likely final plans. Although this is no problem in participatory practice, it is not easily implemented in a simulation lacking facilitation workers and having only hypothetical "generic" actors. We can, however, do the next beat thing and use last year's indicative prices during the first iteration, and then, for subsequent iterations, use a simple algorithm to decide how to correct the median of the proposed total demand and proposed total supply for each good to attain overall balance of all inputs and outputs as if the results were facilitation board generated amounts acceptable for calculating indicative prices via production matrices. A real world system can then do at least as well as our simulation by using this mechanical procedure to calculate indicative prices. It could likely do better using more sophisticated algorithms or relying on actual facilitation workers. Given these elaborate steps, there emerge a number of equations that can help us understand our system.
First, for any normal distribution, the mean times the total number of actors is equal to what we call the "Tot" of the distribution. If we use this relation to consider the demand distribution for a particular good, G, we find
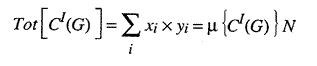
where

is just the total number of consumers.
Temporarily ignoring slack, the value of all goods of type G demanded in any iteration will be
![]()
Likewise, the value of the total net supply of all goods of type G is given
by
![]()
Similarly, the value of all goods of all types demanded will be

So, if we write
![]()
as the vector of all the demand means and
![]()
as the vector of all the supply means, then we have for the value of all goods demanded

And for the value of all goods supplied for consumption

At this point we can also write the value of total producer demand as
![]()
If we assume that for each good we want our slack to be some fixed percentage
of the total net supply of that good, say, for the sake of this discussion,
5 percent, we can write
![]() as
as
![]()
And then
![]()
It ought to be evident from all this that by using these and related expressions, facilitation workers could track and chart many relationships that citizens could examine to help them make their choices. But our primary concern here is tracking what the economy will likely do over the whole planning period and, as a result, the next step is not to delve into how individual actors might use various types of informnation to make their decisions, but instead to determine how groups of people will respond to iterations so that we can go from C1[G] to Ci[G] one step at a time. The most general way to approach this problem is to use the same technique we used with initial consumer response.
Each iteration has its own rules. We assume each iteration will be characterized by some average most probable and frequent behavior so that everyone's behavior will form a distribution characterized by this average as mean and by some particular standard deviation that will vary from good to good.
Suppose we had some rule for a particular iteration constraining the ways actors can alter their prior proposal. Then all the people who had previously said they wanted 300 pints of milk will now re-choose for all goods, including milk, moving up and down in their requests however they decide within the rule constraint. In particular, if we think in terms of a round's distribution of milk demand encompassing the array of ordered pairs (xi,yi), then all the people, yi, who wanted any particular value xi in any particular round will constitute a new group in the following round.
Moreover, each of these new groups will respond to the need to make a new milk proposal from a position of having the same prior milk proposal (though different proposals for other goods) and of confronting the same iteration rules. They will not all do the same thing, of course, but, assuming these groups are large, it is plausible to assume that in going from one iteration to another all the members of a new group will alter their proposals so their new choices will together form a new distribution whose mean is shifted away from their prior proposal for the good by an amount that depends on the rules of the iteration, the projected price for the good, the prior round's status for the good, and the ratio of the prior round's "xi" to the prior round's mean for the good (how far out on the normal curve the group is). The new distribution for all actors' choices for any good, G, will be the sum of the new component distributions for that good and will have a clear relation to the prior distribution which we can deduce in terms of our various distribution functions and relations.
In short, given demand or supply distributions for a good and workable assumptions about behavioral responses to iterative rules in light of anticipated budget constraints, we can create an algorithm able to derive subsequent distributions for later iterations.
For example, assume we have the demand distribution for iteration I for some good G, CI[G] Any consumers who have requested the same quantity of good "G" in round I will constitute a new group for purposes of round I+1.
Moreover, each of these new groups will make choices that will fall on a new distribution curve. The new mean for each group will be moved from the value of the group's prior choice by an amount depending on the good's prior status, the budget, the iteration rule, and the divergence of the group's prior choice from the prior mean for the good. The new standard deviation will be some new value also depending on iteration rules, the good, and the group.
Now, if we let dm stand for the difference between the mean recorded for iteration I+1 and the starting value set in iteration I, the result is that if n people were previously requesting the same amount of a good G in iteration I, in iteration I+1 those n people would be requesting a range of amounts forming a normal curve with mean equal to the prior round's mean plus the change dm The only conceptual difficulty is characterizing dm in terms of relevant factors in a realistic fashion. Having done so, it is merely mathematical manipulation to use the knowledge of how each subgroup of actors might change their choices to determine what will be the change in the overall demand. Moreover, to cover all plausible trajectories at this step we can investigate a range of parametized algorithms.
Given this approach to determining C2(G) given knowledge of C1(G) and the other relevant factors influencing the process, then coupled with our earlier results it becomes possible to track any participatory planning system from first proposal to settled plan in light of whatever choices of rules for each iteration and behavioral assumptions for actors we might wish to consider. This gives us the capability of determining under what conditions and rules outcomes are optimal, acceptable, or unacceptable.
Since all these approaches would work at the level of distributions for the preferences of the entire population and therefore fail to reveal much about the iteration to iteration circumstances of individuals, an additional step might be employed to give feedback about this micro level.
One option, as noted earlier, is to examine a vastly simplified instance in detail by simulating an economy with a limited number of consumers and producers including tracking each individual actor's choices in detail.
A second and more interesting option, however, is to incorporate an individual or a group of individuals into the macro simulation. The individual, or group, would participate in each iteration round at a terminal using data from the whole simulation in the same way that a real actor would use data from the whole rest of a participatory economy. The individual's (or group's) choices would then become part of the data for the new iteration, and so on, to conclusion. This would help clarify the exigencies of individual interaction in participatory planning.
Experiment 2: Developing a Parallel Economy
A simulation incorporates more detail than a differential economic model, but still misses the richness of living interaction. As a result, the full characteristics of participatory economics and the diverse solutions to institutional problems associated with it will ultimately only reveal themselves in actual operations. We will not even know many of the most interesting questions that practitioners might ask until we enact a real participatory economic system. While working to accomplish a revolutionary transformation of existing economies, can any lesser activity intimate more revealingly than a simulation what would happen?
Conceivably one could run a "shadow" participatory economy within an existing economy. This could occur in a subset of the whole economy, whether geographic or by industrial sector, and could be carried out at the level of individuals or groups. Its operations could be evaluated in themselves and also compared to results in the real existing economy. Although this type experiment could be carried out anywhere, it is easiest to imagine in a centrally planned economy with a serious interest in progressive experimentation. In the best scenario, the experiment might expand from one sector to the whole economy and not only serve as a laboratory to test participatory planning, but also as a school, both educating the public and developing the means to implement participatory planning without undue disruption.
What is most important to emphasize regarding this now completed chapter, however, is that the formalism employed here could not only be employed to develop computer simulations, but also improved for use by iteration workers, producers, consumers, and programmers in actual participatory economies or participatory economic experiments.