6.2.2 Round Two: Endogenous Preferences Do Not Matter

If traditional theory, by ignoring endogenous preferences, both misestimates welfare effects and misinterprets the matching of supplies and desires, how can one possibly argue that the conclusions of traditional welfare theory stand intact?

We already demonstrated that a simple correction--completely analogous to the correction introduced by human capital theory-is sufficient to yield theoretically sound estimates of all the welfare effects of economic choices. And while it is possible that desires are molding to supplies, rather than vice versa, it is also possible that relative supplies adjust to relative desires, which themselves are adjusting in an optimal pattern as judged by the overall satisfaction they generate in light of overall possibilities. In other words, while it is possible that a match between relative supplies and desires is merely a sign of social stability, it is also possible that a match is of welfare significance. Theorem 6.2 cautions us not to jump to the conclusion that a good match deserves high welfare marks. But if the match is the result of supplies adjusting to preferences, which themselves are developing along an optimal trajectory, then presumably the traditional practice of awarding high welfare marks is warranted.

It follows that we should now consider whether this superior form of "good match" is, in fact, what private enterprise competitive market economies would yield if they contained no "other" sources of nonoptimality. This entails reexamining traditional welfare theory's three fundamental theorems under the assumption of endogenous preferences.

Below, we present a model of what we will call, for now, a private enterprise, competitive market economy in which people recognize that their preferences are endogenous. This is a general equilibrium, Debreuvian model consistent with all aspects of traditional welfare theory's treatment of such economies except that preferences are treated as endogenous. In other words, no "other problems" are presumed in the model-no "other conditions" besides endogenous preferences that would result in any change in the traditional conclusions. We adopt such a model not because we believe such economies do not have other problems, or that traditional conclusions are warranted, but because we wish to see if endogenous preferences alone reverse any of the fundamental theorems of traditional welfare theory when examined in a general equilibrium seting. ¹⁰ After all, a reasonable reaction to the implication of Theorem 6.2 that matches between supplies and desires are not necessarily deserving of praise is that partial equilibrium conclusions are frequently not sustained by general equilibrium analysis.
It is convenient to adopt the general equilibrium model developed by Debreu in his Theory of Value. Although Debreu's assumption of a fixed number of firms in each industry, perfect knowledge of all future conditions, and treatment of all present and future choices as being made and contracted in the momentary present, are totally unrealistic and crucially misleading to attempts to uncover many mysteries of private enterprise market systems, they are appropriate to our interests of exploring the general equilibrium consequences of endogenous preferences modeled as informed selfdevelopment. We adopt Debreu's analysis of the "production" side of the economy intact, and need only concentrate on implications of endogenous preferences for the "consumption" side. Building on Model 1 of an individual with endogenous preferences, we now define Model 2:

Model 2: A Debreuvian Economy Inhabited by Individuals Aware of Their Endogenous Preferences

M 2. 1. Let {Q, L }ⁱ be the set of all possible consumption/work activity choices over all periods for the ith consumer, where, with Debreu, we assume this set is closed and bounded and therefore compact. Let (q,l)_ij denote a typical (jth) element of this set, and note that such an element specifies a particular amount of each good and each work type in each time period that person i experiences.

M 2.2. Let {C}_i be our name for the set of all possible human characteristics of the ith consumer over all periods. Again, we let c_ij denote a typical element of {C}^_i i remembering that this specifies every human characteristic i has in each time period from

t = 0 ... T.

M 2.3. Let {U}ⁱ be the set of possible "instantaneous" utility functions with U_ij a typical element listing i's instantaneous utility function for every time period.

M 2.4. As in Model 1, M 1.10, let Wⁱ be the overall welfare function for individual i that tells us how much satisfaction i enjoyed over his or her entire lifetime given the amount of satisfaction i experienced in each time period t = 0 ... T.

M 2.5. Since the choice variables for individual i are to select a (q,l)_ij from {Q,L}ⁱ , we can also define an overall well-being function on consumption/work activity space. We define what we explain below is the composite mapping

j = WBⁱ [ (q,l)_ij ] and note that the value of Wⁱ must equal the value of WBⁱ for the same consumption/work activity "history," or the same (q,l)_ij.

Existence of Equilibria. Having specified our model, we prove:

In other words, endogenous preferences, in and of themselves, do not affect the existence theorem for private enterprise market economies except to the extent they undermine the plausibility of the convexity assumption. In the existence proof the crucial questions about preferences concern their insatiability, continuity, and convexity because if appropriate assumptions are postulated in these areas it is possible to demonstrate that individual consumer "demand" correspondences (functions) are upper semi-continuous (continuous). When combined with upper semicontinuous (continuous) supply correspondences (functions) from individual producers and the aggregate production side of the economy, aggregate excess demands for all commodities and work activities can be shown to be upper semi-continuous (continuous) correspondences (functions).

After the appropriate definition of an upper semi-continuous (continuous) correspondence (function) from the price simplex to the set of excess demands and formation of the cartesian product of this set of excess demands with the price simplex, it is possible to apply Kakutani's (Brouwer's) fixed point theorem thereby establishing the existence of at least one general equilibrium. Once upper semi-continuity (continuity) of the excess demand mappings is established, the remaining steps in the existence proof are well known and we can leave interested readers to consult familiar formulations. ¹² We, therefore, need only concern ourselves with the upper semi-continuity (continuity) of individual consumers' demand correspondences (functions).

INSATIABILITY: The traditional view of the insatiability assumption is misleading in its focus on a tautological and obvious aspect of the human condition, namely that more of something good is better than less, and its neglect of a more intriguing aspect of the human condition, namely that each of us has only a limited amount of time to undertake our consumption and work activities so that engaging in "more" of one activity has an opportunity cost in terms of other activities that must be foregone. But this problem need not concern us here. For nothing about endogenous preferences changes the reasonableness (or unreasonableness) of the insatiability assumption. Specifically, there is no more reason to question the insatiability assumption for our well-being functions than for Debreu's traditional preference orderings, both of which are defined on the sets {Q, L}ⁱ.

CONTINUITY: Although a number of technical details must be analyzed concerning continuity of the correspondence from the set {Q, L}ⁱ to the "possibility" set for an individual consumer with a given vector of initial endowments and "stock" ownership under a given price system, assuming endogenous preferences does not affect any of these details.¹³The important issue is how to conceptualize the process of character formation and derivation of satisfaction from consumption-work choices. We have already motivated an approach that envisions activities in one period as affecting human characteristics in subsequent periods and satisfaction as depending on the state of one's human characteristics as well as one's activities. Obviously, nobody can hope to specify the precise functional nature of these incredibly complex cause-effect relations. To do so would imply that psychologists had solved all the problems of their discipline! And for most purposes it is probably inappropriate to view these relations in precise, mathematical, functional forms. Yet there is a long tradition among welfare economists of treating complex psychological processes as if they could be modeled in precise mathematical ways. The lack of hubris is justified on the basis of the nonintuitive insights gained. In this spirit we postulate that the mapping of human characteristic formation from {Q, L}ⁱ to {C}ⁱ is continuous, and that the mapping from

{ {C}ⁱ ; {Q, L}ⁱ } to {U}ⁱ is continuous. At least there is nothing intrinsic to endogenous preferences that precludes this. In which case, we can conclude that {C}ⁱ is compact since {Q, L}ⁱ is compact and the mapping is continuous; that

{ {C}ⁱ ; {Q, L}ⁱ } is compact since the cartesian product of two compact sets is compact; that our utility set, {U}ⁱ is compact since a set of elements generated by a continuous mapping from a compact set is compact; and finally, that our overall welfare function, Wⁱ is a linear, continuous function defined on the compact set, {U}ⁱ Hence the composite "wellbeing" function, WBⁱ, mapping directly from {Q,L}ⁱ space to the set of real numbers giving us what we interpret as the individual's well-being is continuous. In sum, our well-being function, WBⁱ that is expressive of perfectly informed endogenous preferences, can be reasonably attributed the same continuity properties usually assumed for exogenous utility functions. At least there is nothing inherent in the notion of endogenous preferences to indicate otherwise.

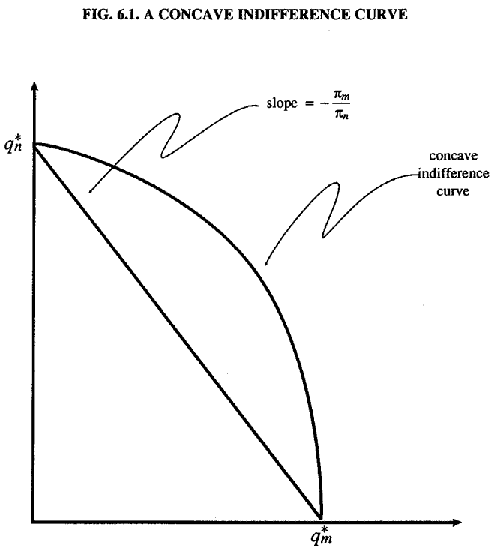
CONVEXITY: From the diagram in Fig. 6.1 we can see that some form of convexity is necessary to assure continuity of an individual's demand correspondences. If the set of consumption/work activity bundles preferred to a given bundle is concave, as pictured above, a slight shift in relative prices of two items can produce a "jump" discontinuity in demand for those goods. In this case, a shift in the relative prices from

for e > 0 would produce a change in demand from (q_n*, 0) to (0, q_m*). The question, therefore, reduces to whether or not it is inherently less reasonable to assume the set of bundles giving equal or greater well-being according to our endogenous preference well-being function is convex, than to assume that the set of bundles giving equal or greater utility according to an exogenous preference utility function is convex. Does endogeneity of preferences increase the likelihood of concave indifference curves like that pictured in Fig. 6.1?

If we grant the assumption of convexity, then taking it together with the continuity and nonsatiation assumptions, it can be deduced that every individual consumer's demand correspondences are continuous. ¹⁴ unfortunately, it would appear there are additional reasons to fear non ' convexities once we recognize preferences are endogenous to economic choices.

It has been argued that all convexities are the consequence of some form of indivisibility, since the full benefits of something can only be realized when a certain amount is consumed, this amount being greater than a single unit. ¹⁵ Of course, all nonconvexities could be eliminated by appropriate redefinition of the unit of account, but unfortunately, this "way out" produces equally disconcerting problems in the form of discontinuous preferences over the new units and ultimately complicates the question of whether markets can reasonably be assumed for all commodities and work activities in the units as we newly define them. One is free to redefine units of account but not free to assume that units that are convenient for eliminating nonconvexities will necessarily coincide with units convenient for purposes of continuity of preferences and existence of markets.

One of the implications of the paradigm we developed in chapter 5 is precisely that there are excellent reasons for believing that the real human world is not such that so happy a coincidence results. Moreover, our paradigm is quite consistent with mainstream modern social theory, which recognizes that the content of social structures cannot be reduced to the sum of separate individual participations. And while few economists realize the implication, the interactive view of society entails widespread opportunities for nonconvexities. ¹⁶ So, rather than being "neutral," the traditional welfare paradigm flies full in the face of mainstream social theory by projecting the kind of individualism necessary to justify the assumption of convexity.¹⁷

But the additional cause for concern about nonconvexities in consumers' preferences due to endogenous preferences is more mundane. One of the few reasons for nonconvexity that has received attention from traditional theorists is increasing returns to scale. As soon as consumption is recognized as having an "investment" aspect in changing human characteristics, more serious concerns of indivisibility in the form of increasing returns become apparent.
To cite one example, the immediate satisfaction derived from taking music lessons might exhibit diminishing returns, but the longer term benefits derived from further "investments" in music lessons now, in the form of appreciation of symphony concerts over one's entire life, could easily exhibit increasing returns over lengthy periods of consumption. The conception of endogenous preferences as myopic habit formation suggested by von Weizsacker and studied by Pollak and others is another obvious example. Although arguments have been advanced concerning diminution in the size of the discrepancy from equilibrium for a given nonconvexity as the size of the economy increases, it is well recognized that nonconvexities prevent demonstration of the existence of general equilibria. ¹⁸ In any case, our demonstration of Theorem 6.3 is complete under prescribed, admittedly dubious, conditions.
But we waive the fight to quibble over existence theorems in order to focus on more substantive issues. We are happy to interpret Theorem 6.3 as extending the first fundamental welfare theorem: Equilibria exist under the usual assumptions, even if we treat preferences as endogenous. But will equilibria in a competitive, private enterprise market economy be Pareto optimal if preferences are endogenous?

Pareto optimality .

In other words, treatment of preferences as endogenous does not affect the conclusion that any general equilibrium of a perfectly competitive, private enterprise economy is a Pareto optimum provided all other traditional assumptions hold. Endogenous preferences, of themselves, do not affect the efficiency theorem for private enterprise market economies.

The proof of this theorem is well known, and the critical assumptions are the absence of externalities and "thick" indifference classes. ¹⁹ The absence of "thick" indifference curves is necessary to assure equivalence of the statement that a particular consumption/work activity bundle maximizes WBⁱ subject to the individual i's budget constraint and the statement that a particular consumption/work activity bundle minimizes expenditure required to achieve a given level of well-being. Absence of externalities is necessary to assure that if particular consumption/work activity bundles for each consumer and particular input/output vectors for each firm minimize a certain function on appropriately defined sets for each actor, their sum will minimize that function on the sum of those individual sets. If there were any externalities, the possibility would arise that a particular choice from one actor's set would change the production possibility set for some other firm or the "at least as preferred to" consumption set for some other consumer, and therefore, the independence of all actor's sets must be postulated. It is well known that no convexity assumptions, either for production possibility sets or "at least as preferred to" consumption sets, are required for the derivation since the existence of an equilibrium is hypothesized in this theorem, so related reservations are irrelevant in this proof. Since we postpone "other" problems with private (and public) enterprise market institutions until later chapters, here we can accept familiar assumptions regarding the nature and meaning of "competitive" labor markets and the absence of externalities. Therefore, our continuous, endogenous preference well-being functions, WBⁱ which admit of no satiation activity bundles, are sufficient for the proof of Theorem 6.4 via the usual argument. While nonconvexities in the "equal to or greater than" well-being providing consumption/work activity sets may render the optimality theorem vacuous by making it impossible to prove the existence of an equilibrium, convexity considerations play no direct role in the optimality theorem.

Distributional Flexibility. We can now complete our resurrection of traditional welfare theory's holy trinity of fundamental theorems by proving:

In other words, endogenous preferences, in and of themselves, do not affect the flexibility theorem for private enterprise market economies. Once again, the proof of this theorem in the case of exogenous preferences is well known. ²⁰ In this case, "all the usual assumptions" include assumptions necessary for both Theorem 6.3 and Theorem 6.4. We must assume appropriate convexity properties to guarantee existence of equilibria and we must assume absence of "thick" indifference curves, accept the traditional characterization of labor markets, and stipulate the absence of externalities, to be sure the Pareto optimum can be reached via a general equilibrium. But beyond noting the need for these assumptions, there is nothing new to be discussed about their character in the case of Theorem 6.5. We have already stated that nothing intrinsic to endogenous preferences precludes accepting traditional assumptions concerning externalities and "thick" indifference curves. We have also already discussed how endogenous preferences generate well-being functions, WBⁱ, for which "at least as preferred to" consumption and work activity sets of individuals may not be convex. Waiving objections to the convexity assumption that endogenous preferences do make less plausible, Theorem 6.5 extends the traditional conclusion of distributional flexibility of private enterprise market economies under the assumption of endogenous preferences.

Interpretation of Theorems 6.1 Through 6.5.

Our resurrection of all three cornerstones of traditional welfare theory under perfectly informed endogenous. preferences is complete. Under the usual assumptions the existence and optimality of an equilibrium for any competitive, private enterprise market economy is assured, and any Pareto optimum can be achieved as the equilibrium of a competitive, private enterprise market economy with the appropriate initial endowments even if preferences are endogenous. Moreover, in the process of reestablishing the fundamental theorems, we have alleviated any anxiety about the implications of multiple equilibria.

Gintis believed endogenous preferences made multiple equilibria far more likely. Apparently he assumed many of these equilibria would not be Pareto optimal , since he argued that efficiency would require a Central Planning Board to choose among the equilibria and promulgate the set of prices and wages necessary to generate a socially efficient equilibrium. But Theorem 6.4 clearly states that should there be multiple equilibria they would all be Pareto optimal under the usual assumptions. ²¹ So there is no need to append a Central Planning Board to a Debreuvian free market economy whose inhabitants are perfectly informed regarding their own particulars to "guarantee" the "correct" equilibrium. Were a Central Planning Board necessary, this would certainly violate the spirit of a free market system. But Gintis' "technical" critique of private enterprise market econ omies based on the greater likelihood of multiple equilibria under endogenous preferences, which he erroneously believed implied a need to centrally plan such an economy in any case, disappears under the assumption of individual perfect knowledge.

Theorem 6.2 certainly points out the necessity of extending the insights of human capital theory to preference development and falsifies the usual "separability" assumption necessary to justify partial equilibrium applications of neoclassical welfare theory. But, more importantly, Theorems 6.3, 6.4, and 6.5 reestablish traditional welfare conclusions concerning relations between competitive equilibria of private enterprise market systems and Pareto optima in context of endogenous preferences. It appears we have formally confirmed what were only speculations for von Weizsacker, Pollak, and Hammond-taken alone perfectly informed endogenous preferences do not affect fundamental conclusions of traditional welfare theory. In Kuhn's language, were we to stop here, our demonstration of Theorems 6.3, 6.4, and 6.5 might well be interpreted as "normal scientific development" in which the traditional paradigm accommodates to a more general context in which old conclusions are reaffirmed.

6.2.3 Round Three: Endogenous Preferences Do Matter

Appearances can be deceiving. Let us clarify the meaning of Theorems 6.3, 6.4, and 6.5 . If we assume no other aspects of private enterprise, competitive market economies produce nonoptimalities, treatment of preferences as endogenous does not affect the fundamental theorems of traditional welfare economics. Put this way, and with the benefit of hindsight, we might consider the result hardly surprising. If private enterprise market systems were totally flexible and efficient in meeting people's desires, why should they not be totally flexible and efficient satisfying people's preferences for alternative desires themselves? Why shouldn't a system that gives people what they care about, in proportion to the degree they care about it, give people the desires as well as the goods they want? Indeed, upon reflection, it would be surprising if treating preferences as endogenous, by itself, could affect the optimality properties of any economic system. This may explain von Weizsacker, Pollak, and Hammond's confidence in their speculations.

Suppose we generalize and then state our growing suspicion as a hypothesis. For any possible economic system we can ask whether the system has an equilibrium (or generates a feasible plan) and call this the existence theorem for the system. If the system does have at least one equilibrium, we can ask if any equilibrium (or feasible plan that results) will be a Pareto optimum and call this the optimality theorem. Finally, we can also ask if the system, under some arrangement, is capable of generat ing any Pareto optimum and call this the distributional flexibility theorem. Our analysis suggests as a hypothesis that moving from treating preferences as exogenous to treating them as endogenous will not, in and of itself, affect the truth value of these fundamental theorems for any economic system.

But even should this hypothesis prove true, it would not necessarily mean that endogenous preferences "do not matter." For example, if endogenous preferences have a profound effect on how and to what extent "other" problems generate nonoptimalities, then they certainly "do matter." In fact, it is possible that treating preferences as endogenous can completely change our view of why and how different economic institutions facilitate or obstruct well-being even though, in and of themselves, they do not affect the three fundamental theorems of welfare economics. This is the case we now argue.

Theorem 6.2 suggests the kind of results we will present in this section. We interpreted Theorem 6.2 earlier as meaning that rational people will adjust their desires to accord to expected future availabilities. Theorem 6.4 demonstrated that in a general equilibrium context this does not preclude optimality. But this leaves open the possibility that while endogenous preferences do not create nonoptimalities in and of themselves, they may magnify misallocations that appear for other reasons. Before treating this possibility, we must examine Theorem 6.4 once again, because in spite of the "careful restatement" above, our interpretation of Theorem 6.4 is still potentially misleading.

We interpreted Theorem 6.4 as if it had to do with the optimality of a private enterprise, competitive market economy. In fact, Theorem 6.4 has nothing whatever to do with a private enterprise market system. By assuming away "all other problems" in a private enterprise market system, we created-by supposition-a system with no inefficiencies, a system with no distortion of the conditions of availability of different economic activities, a system with no biases in the conditions of relative supplies of different consumption goods and laboring activities. Whether or not even the most perfectly competitive private enterprise, market economy can justifiably lay claim to such qualities remains to be discussed. In fact, the main purpose of next two chapters is to resolve just this claim.
Yet this is not to say the assumption of "no other problems" was ill formulated. In light of the claims and counterclaims made about the effect of endogenous preferences, in and of themselves, on the optimality properties of private enterprise market economies, the assumption of "no other problems" was critical to laying this debate to rest. But the economy we created for this purpose-and interpreted as a private enterprise market system in which we agreed to ignore all problems other than endogenous preferences-can be more accurately interpreted as a hypothetical economy with no distortions, biases, or inefficiencies built into its institutional structures. In other words, the economy we analyzed in Theorem 6.4 was not defined by the particular institutional structures of private enterprise and competitive markets. It was not defined by any institutional structures at all. It was instead defined by the presumed absence of any distortions or biases in the conditions of availability of different economic activities.

While we pretended for the sake of a particular argument that this could occur within the institutional structures of private enterprise and competitive markets we had no reason to believe this to be the case, other than traditional attitudes. Whether or not particular institutions merit the distinction of introducing no distortions or biases is the subject matter of part 3 of this book. What we created in Theorem 6.4 was an ideal "marshmallow economy" subject only and entirely to people's desires for goods and laboring activities and their preferences for different desires once treatment ²² of preferences as endogenous allowed these to be expressed.

What we discovered in Theorem 6.4 now appears rather trivial: A perfect "marshmallow" economy that adjusts only and entirely to people's economic "wills" will generate socially efficient outcomes under the assumption of endogenous preferences just as it did under the assumption of exogenous preferences. ²³
But what would be the effect of introducing endogenous preferences in a less ideal setting in which particular economic institutions do distort the availability of economic activities? Obviously, in any chosen economy that displays a bias we will find inefficiency. But will a treatment of preferences as endogenous give us a different view of the character and consequences of such inefficiencies? Theorems 6.6, 6.7, and 6.8, below, say yes, and reveal the real significance of endogenous preferences.

Theorem 6.6 addresses the effect of perfectly informed endogenous preferences on nonoptimal allocations arising from bias in the relative terms of supply of economic activities.

Theorem 6.7 addresses the effect of perfectly informed endogenous preferences on nonoptimal human development trajectories arising from bias in the relative terms of supply of economic activities.

Theorem 6.8 addresses the impact of ignoring informed endogenous preferences on analysts' ability to perceive the effects of economic biases.

Preliminary Discussion of Theorems 6.6, 6.7, and 6.8

First, we must define the concept "degree of nonoptimality." Beyond judging situations to be Pareto optimal or non-Pareto optimal , we wish to judge whether situations are closer or farther from a particular Pareto optimum. We define "degree of nonoptimality" as the divergence of actual relative supplies from the relative supplies that characterize the optimal production program. The degree of nonoptimality is measured in commodity and not utility space. "Snowballing nonoptimality" occurs when the divergence of actual from optimal relative supplies grows larger in successive time periods.

We must also define "warped human development pattern." Any outcome or "solution" in a multiperiod Debreuvian model consists of activity choices in all time periods, But in a model in which people have endogenous preferences, any solution also implies a particular pattern of development of human characteristics for each individual, along with the instantaneous preferences that depend on them. In other words, a human development outcome accompanies each activity outcome. The human development patterns that accompany activity outcomes that correspond to Pareto optima, we term "optimal human development trajectories." Human characteristic patterns that accompany activity outcomes that are not Pareto optimal , we describe not only as "nonoptimal," but as "warped" because, as we will see, they are "self-generated" by conscious choice in light of perfect information. If actual human characteristics deviate from optimal human characteristics to an ever greater extent in successive time periods, we say the "warping" of human characteristics "snowballs."

Finally, discussion of the model and the demonstration is in order. The fact that we grant people in our economy immortality by assuming that

t = 1,2, ... ¥ might appear objectionable. Besides being of generous disposition, we did this because it is more convenient than choosing "cut-off ' times when dealing with "snowballing" phenomena. As people adjust in earlier periods to conditions previsioned in later periods, cut-off times that imply a diminution of the snowballing as people near the end of their appointed times would introduce unnecessary complexities. The problem is analogous to evaluating investment stocks in the final years of national planning models so familiar to economic planners, and we do not believe eliminating this complexity invalidates our results.

We also focus on only four activities and two human characteristics because this is all that is necessary. From all activities we specify that only two have what we call "developmental effects" in the sense that engaging in these activities in an earlier time period affects one's human characteristics in later time periods. And we specify that the preferences for only two other activities are "affected developmentally" in the sense that one's preferences for these activities are influenced by human characteristics that can be influenced by prior activities engaged in. The conclusions of Theorem 6.6 result if there is a bias in the relative conditions of supply individuals face for the two activities for which preferences can be "affected developmentally." If activities with "developmental effects" and activities that can be "affected developmentally" are more widespread, the "snowballing" nonoptimality would obviously be more pervasive.

We specify the single bias in the economy as follows: we assume that no productive resources are left idle, that only technically efficient methods of production are employed, and that no exchange of inputs between production units could increase the output of one without decreasing the output of another.²⁴ We also assume the economy supplies all activities in such quantities that the marginal social cost of producing the last unit is equal to the market demand for the activity, and that market demand is the sum of demands of individuals with a limited income out of which they purchase economic activities according to their preferences and developmental capabilities. For all goods but one the economy "charges" individuals the net marginal social cost of supplying each person with another unit of the activity. ²⁵ The single bias is defined as a charge in excess of net marginal social cost of supply to the individual purchaser of one of the activities that can be "affected developmentally."

Demonstration of a degree of nonoptimality greater than envisioned by traditional welfare theory that "snowballs" over time amounts to showing that the total supply of the activity subject to the charge in excess of net marginal social cost, relative to the total supply of other activities, will be less than calculated assuming exogenous preferences and grow less over time. Our formal demonstration works backward and then forward again in time, mirroring the "logic" of a "rational" individual confronted by a change in the future relative conditions of supply from the "optimal" ratio to the "biased" ratio. Unfortunately, our result is not easily proven formal ly. We must examine five different conceivable reactions an individual might adopt to introduction of a bias in the conditions of supply. Moreover, of the four possibilities we must exclude to demonstrate our result, the most intuitively absurd proves the most difficult to exclude formally.

Model 3: An Economy with a Single Bias in the Conditions of Supply Inhabited by Individuals Aware of Their Endogenous Preferences.

Model 3 is a simplified version of Model 1 deleting all unnecessary complications. It is only necessary to consider four activities and two characteristics, and we abstract from human capital "earnings" effects altogether. But characteristic formation functions, as well as instantaneous utility functions are assumed to be continuous and differentiable, as well as having the other "traditional" properties described below.

M 3. 1. There are many people: i, j = 1, 2, ...N (finite), and many time periods: t = 1, 2, ... ¥.

M 3.2. There are four activities in each time period: three activities, x, y, and z which are made available to individuals at prices equal to their net marginal social costs; and one activity, a, for which individuals are charged in excess of net marginal social cost.

M 3.3. There are two human characteristics in every time period that can be "affected developmentally" and "parameterize" the "instantaneous" utility functions.

We specify these relations for i = 1...N; t = 0 ... ¥ k = 1 ...¥ by

M 3.4. For good x and individual i:

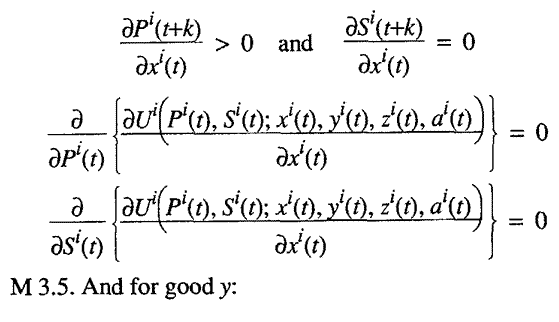
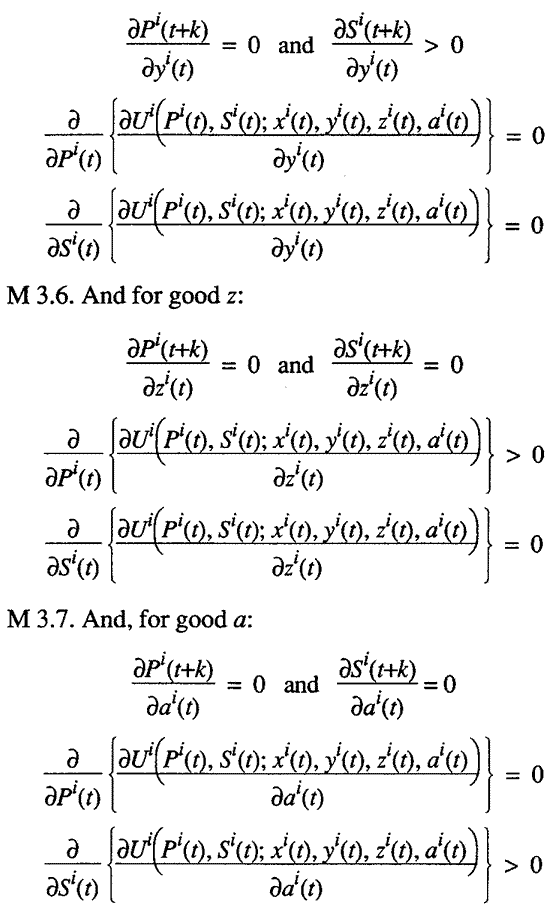
M 3.8. People have "instantaneous" utility functions in every time period, U_i(t), and an overall well-being function that is a linear sum of utilities achieved in each time period with all weights equal to 1. ²⁷ Thus individuals are assumed to maximize:

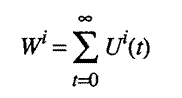
where, as above, for all i and t:

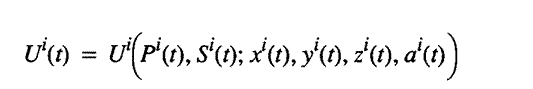
M 3.9. The single bias in the economy is specified by charging individual purchasers of x, y, and z the net marginal social cost of providing them the activity, but charging those who purchase a some amount in excess of the net marginal social cost. To reflect this, we can let 0 = O(x(0), y(0), z(0), a(0); ... x(t), y(t), z(t), a(t); ... ) define the traditional production transformation locus of all efficient productions for the economy as a whole. Then the ratios of the marginal social costs of producing one more unit of b at time t in terms of the number of units of c that must be foregone at time (t+k) would be

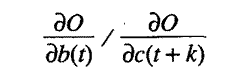
where b and c can equal x, y, z, or a; t = 0 ...¥; and k = 1 ...¥

M 3.10. We further define the ratios of net marginal social costs to society of making activities available to individual i. The ratio of the net marginal social costs of supplying one more unit of b to i at time t as compared to supplying i with one more unit of c at time (t+k) is: ²⁸

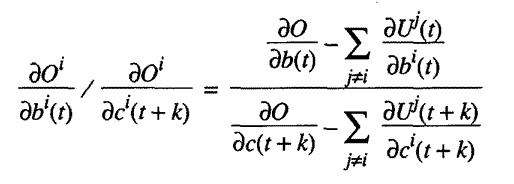
M 3.11. Since we have stipulated that supplies will be responsive to market demands in our economy, our economy must charge individuals an amount equal to the net marginal social cost of supplying each person with another unit of any activity if the economy is to be efficient. ²⁹ Whereas our economy does so for activities x, y, and z, for activity a it charges some amount in excess of net marginal social cost. We specify all this for time period (t+k) in the following equation where superscript A stands for "actual" and superscript O stands for "optimal."

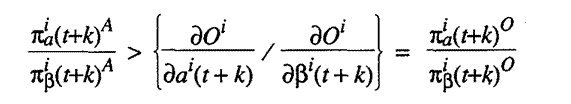
where b = x, y, or z