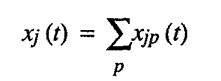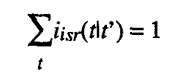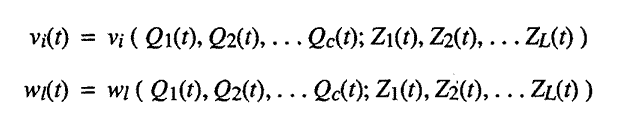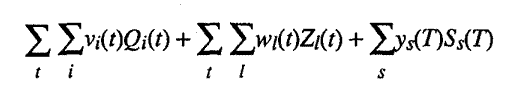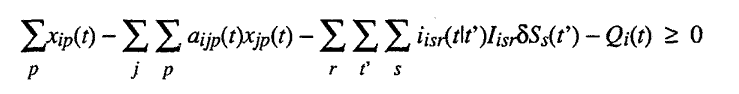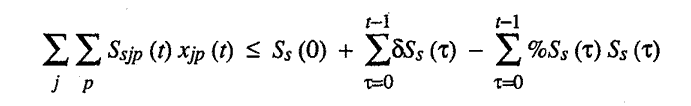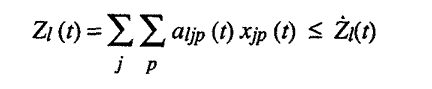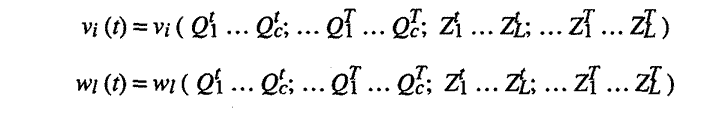A
Quiet Revolution in Welfare Economics- by Michael Albert and Robin Hahnel
9
CENTRAL
PLANNING
WE BEGIN by reviewing the "old" debate about whether or not central planning
can be efficient. In the context of modern mathematical programming techniques
and computer capabilities, the "old" debate, brought into focus by Barone's
essay "Ministry of Production" published in 1908, has been resolved in the affirmative.
1 We will extend this conclusion to the
case where individuals' preferences are endogenous. But the "old" debate assumed
that the Central Planning Board would have perfect knowledge of all resource
availabilities, all technical capabilities of all production units, and society's
social welfare function, and that all the Central Planning Board's instructions
would be carried out.
Next we review the "modern" debate about information gathering difficulties and
incentive problems in central planning. We analyze a number of iterative techniques
designed to help the Central Planning Board gather technical data from the separate
units in the economy. We review a number of approaches to formulating society's
social welfare function. And we discuss incentives that might be used to induce
managers and workers to carry out the plan once it is calculated. We conclude
that many information and incentive problems emphasized by critics of central
planning are resolvable, and that the most intractable problem-obtaining accurate
information from management about productive capabilities-is not unique to centrally
planned systems.
Having reviewed the "old" and "modern" debates-both conducted in terms of traditional
welfare theory-we reevaluate the different iterative techniques for gathering
technical information using our new welfare criteria and discover that all these
techniques are cybernetic disasters from a social point of view, regardless of
how successful they might be for informing central planners. This leads to our
first new criticism of central planning: as necessary as consolidating data from
individual production units in the hands of central planners might be for central
planning to achieve efficiency, the primary cybernetic task of economic institutions
appropriate for achieving self-management is to disseminate information about
other production units so the members of each unit can expand their understanding
of how their choices impact on others and vice versa. The techniques for processing
information in central planning not only fail to do this, but accomplish just
the opposite.
Next we discuss the roles inherent in central planning using our new evaluative
criteria. We find the interunit roles to be irresolvably authoritarian and discuss
the likelihood that their authoritarianism would spread to intraunit roles as
well. We point out that apathy is the other side of the authoritarian coin and
that the roles defined by central planning relegate individual production units,
and most often workers within those units, to just such a condition. In this respect
our work provides a theoretical basis for criticisms often voiced by analysts
of central planning in practice.
But our most important new criticism of central planning derives from reanalyzing
the problems associated with estimating society's social welfare function. We
discover that central planning is incapable of providing selfmanaged work activities
in accord with their true social opportunity costs. Even giving central planning
every benefit of the doubt---eliminating the Central Planning Board from any decision-making
role, formulating the social welfare function through strictly democratic procedures,
and including different kinds of work activities as well as different final goods
in the social objective function to be voted on-we find that central planning
is inherently biased against supplying self-managed work roles.
Worse still, treating preferences as endogenous we prove that central planning's
inherent bias against supplying self-managed work activities leads to a "snowballing
divergence" from optimality in which the economic plan proceeds farther and farther
from an optimal use of society's laboring capacities as time goes on. When viewed
in terms of human development, this snowballing divergence displays itself as
an ever-increasing apathy of the executors of economic activities as they accommodate
to the absence of opportunities for self-managed work activities.
We conclude with some observations on how the institutions of central planning
might be expected to affect the disposition of classes in public ownership economies.
We suggest that the institutions of central planning contribute to the development
and strengthening of a coordinator class separate from, and with interests opposed
to, ordinary workers in such economies.
9.1 A Centrally Planned
Public Enterprise Economy
We begin with a moderately complex model that could be used to calculate a central
plan for an economy.
9.1.1 Model 4: The Central Planning Problem
M 4. 1.
The time horizon for the plan in Model 4 is t
= 1, 2, ... T.
M 4.2.
The gross outputs of produced goods i and j in period t
are xi
(t) and xj(t)
respectively, where i, j
= 1, 2, ... c.
M 4.3.
The number of different processes for making good i
are p
= 1, 2, ... P(i). The number of different ways to add
to capital stocks are r
= 1, 2, ...R(s).
M 4.4.
There are L different
kinds of labor and primary (nonproducible) factors of production, l
= 1, 2, ...L, and for each time period there exists a certain
amount of each of these factors including man/woman hours for labor categories
and physical quantities for land, minerals, etc. The available supplies are
taken as "given." Zl(t)
stands for the amount of factor I
available in period t
. Zl (t) stands for the amount of factor l
actually used in the production program in period
t .
M 4.5.
xjp(t)
stands for the amount of good j
produced in period t
via process p.
The total amount of good j produced
in period t
is:
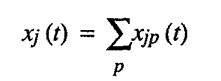
M 4.6.
aijp(t)
stands for the amount of i
needed to make one unit of j
via processp in period t
.
M 4.7.
Ss(t)
stands for the stock of capital good s
in existence at the outset of period
t , where s
= 1, 2,...m < c.
M 4.8.
dSs(t)
stands for the addition to stock of capital good s
in period t . And
%Ss(t)
stands for the fraction of capital good s
that physically depreciates in period
t , which we assume to be independent of usage.
M 4.9.
aljp(t) stands for the amount of primary factor
l needed to make one unit of good
j via process p
in period t
.
M 4. 10.
Ssjp(t)
stands for the amount of stock of capital good
s we must have on band to produce one unit of good j
via process p in
period t .
M 4.11.
lisr stands for the total amount of good
i that must be set aside (invested) in all prior periods to
obtain one unit increase in the stock of capital good s
via process r.
M 4.12.
iisr(tlt') stands for the fraction
of Iisr that
must be invested in period t
to help produce one more unit of capital good s
in later period t '
via process r. Thus,
[iisr(t|t')]
[Iisr] stands for the amount of i
that must be set aside in period t
to help get one more unit of stock of s
in period t '
via process r,
where:
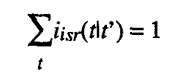
M 4.13.
Qi(t)
stands for the final consumption of good i
in period t .
The Central
Planning Board is provided society's "social welfare function" containing society's
relative valuation of all final consumption goods and labor activities.2
The simplest case would be a linear social welfare function where vi(t)
stood for the relative social value of one unit of consumption good i
at period t , and where
wl(t)
stood for the relative social value of one unit of primary factor
I at period t
. For all l that
correspond to a specific kind of labor activity, the wl(t)
would represent the relative disutility of performing an hour's worth of that
activity. For all l
that stand for nonlabor primary factors there is no reason they would not
have wl(t)'s
equal to zero, for even with T
a finite time period, we do not accumulate stocks of these nonproductive inputs
in our model; they simply appear in certain quantities each time period, and would
presumably do so in the future.
In the case of a finite time period, however, we would have to set some positive
social values on the different stocks of produced goods in the last time period
if we are not to totally ignore the well-being of generations to live after time
period T .For now, assume
the planners know the valuations for capital goods
s, ys(T) as well.
An easy way to handle the more general case of a nonlinear social welfare function,
where the relative social value of a unit of any final good or labor activity
depends on both the absolute and relative amount of the good or activity that
was being consumed, would be to simply interpret the vi(t)'s
and wl(t)'s
as functions of all the Qi(t)'s
and Zl(t)'s.
M 4.14.
That is
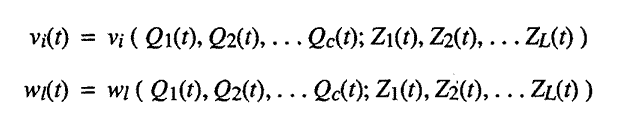
where this formulation allows for the usual substitutes and complements. Finally,
we are ready to state the Central Planning Board's programming problem: Maximize
social welfare
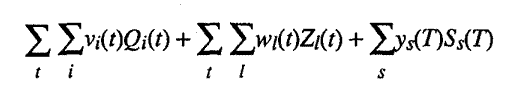
subject
to the following constraints:
1. Producing
enough of each good in each year to meet its intermediate, investment, and
final consumption uses as expressed by the cXT
inequalities
(for i
= 1, 2,... c and
t = 1, 2,... T):
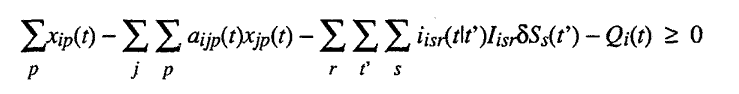
2. Having at least the minimum amount of all the necessary capital stocks
available at each time period for the production of each good as expressed
by the mxT inequalities
(for s=
1.... m and t = 1,...,T):
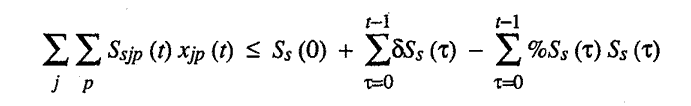
3. Having
at least the minimum amount of all the necessary primary, nonproducible factors
like labor, land, etc., available at each time period for the production of
all goods as expressed by the L
x T inequalities (for
l = 1, 2,... L and t = 1, 2.... T):
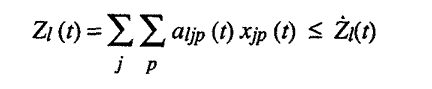
For this
problem, the givens are the aijp(t)'s,
aljp(t)'s, Ssjp(t)'s, iisr(tIt')'s,
Iisr's, and %Ss(t)'s, which
are production, investment, and depreciation coefficients; and the
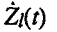 's
and Ss(0)'s,
which are stocks of primary factors and initial capital goods; and the vi(t)'s,
wl(t)'s and ys(T)'s, which
are the relative values of different goods, work activities, and final stocks.
The "decision" variables for the Central Planning Board are the
xjp(t)'s and the Qi(t)'s,
which imply the ZI(t)'s
and Ss(t)'s.
's
and Ss(0)'s,
which are stocks of primary factors and initial capital goods; and the vi(t)'s,
wl(t)'s and ys(T)'s, which
are the relative values of different goods, work activities, and final stocks.
The "decision" variables for the Central Planning Board are the
xjp(t)'s and the Qi(t)'s,
which imply the ZI(t)'s
and Ss(t)'s.
9.2 Round One: Efficiency
of Central Planning
9.2.1 Calculating the Plan
Although the only feature essential to our purposes is that the planning model
be multiperiod, we have included a limited number of complications that hint at
the complexity any realistic situation entails. Model 4 allows:
1. Planning
over many time periods
2. A number
of different nonproducible, or primary inputs, including different kinds of
labor services
3. The
necessity of having stocks of different "capital" goods in place as well as
intermediate and primary inputs for production to take place
4. A variety
of different production techniques for producing a variety of different intermediate
and final goods
5. A variety
of different processes by which the stocks of "capital" goods can be increased
allowing variation in inputs and in the timing of their application
Although we included in Model 4 the possibility that different kinds of labor
activities might have different effects on social welfare, and will discuss this
case in a later section, the "traditional" debate about the efficiency of central
planning considered only final consumption goods to be of welfare significance.
It treated different categories of labor only as limiting primary factors. Model
4 can be easily adapted to the "traditional" debate by excluding the second set
of terms in the planning board's objective function in the definition of the planner's
problem.
The central planner's problem can be formulated as a linear programming problem
where the different social evaluations of final goods are presumed constant and
production technology is presumed to exhibit constant returns to scale. In the
more realistic case of relative valuations of final goods being functions of relative
amounts of final goods provided, and nonlinear production technologies, two approaches
are available.
We could reformulate the planning problem as a nonlinear programming problem in
either the objective function, the constraints, or both. Or more practically,
we could incorporate the more realistic elements within the framework of linear
programming by using a variety of well-known artifices. To account for economies
of scale within a linear framework one can define new activity vectors and new
units of output for larger and smaller scale operations. To account for nonlinear
social preferences one can define new variables in the objective function for
different ranges of output and introduce new constraints limiting the range of
possible values these new output variables can take. In this case Model 4 can
be interpreted as allowing for these additional elements of realism within a linear
framework.
But whether we use artifices to retain linear forms, or explicitly formulate a
nonlinear programming problem, solutions maximizing social welfare, and a number
of algorithms for finding them, are known to exist,
3 and there is no need to belabor these technical matters here.
The point is that in light of modern mathematical programming theory and computer
capacity, the "old" debate about whether a centrally planned economy
can be efficient is settled in the affirmative provided one can assume the planning
board
1. Has
perfect knowledge of initial capital stocks and primary resource and labor
availabilities
2. Has
complete information about the technical coefficients of all the different
production processes
3. Possesses
an accurate social welfare function to be used as the objective function in
the programming problem
4. Has
a sufficiently large computing facility
5. Will
have its plan carried out
The "modern" debate about the efficiency of central planning has revolved precisely
around whether or not these assumptions can be justified. But before considering
various schemes for solving information and incentive problems in centrally planned
economies, we first need to address the distribution of final goods among the
different consumers and the assignment of particular individuals to specific jobs.
For while a Central Planning Board might achieve a socially optimal production
plan, this does not guarantee Pareto optimality unless the assignment of work
and distribution of final goods is also carried out efficiently.
When the Central Planning Board calculates an optimal plan, it arrives at a complete
list of all the inputs each unit is to receive and the outputs each unit should
produce. Included among the list of inputs are the number of hours of different
categories of labor services that each unit is to use, but this is not the same
as a list of who will be assigned to which units. Similarly, when the amount of
each product needed in production and for investment is subtracted from the gross
output of that good we arrive at the net output of each good available for consumption.
But this is not the same as a list of the amounts of each final good to be distributed
to each consumer. In other words, even if we assume that an optimal plan has been
calculated and carried out, some system of distribution of final goods and job
assignments is needed. Obviously inefficiencies could arise in these aspects of
a centrally planned economy as well. Next we describe a few ways by which distribution
and job assignment could be carried out, along with the necessary conditions for
them to achieve Pareto optimality , to illustrate just how markets are, and are
not, related to efficiency in central planning.
9.2.2 Distribution of final Goods
1. The
Central Planning Board could distribute arbitrary portions of each final good,
in each time period, to each member of society.
Of course giving equal portions of each good in each time period to each citizen
would be one such distribution. But less egalitarian possibilities abound. To
preserve optimality under any chosen scheme, all citizens would have to be free
to trade whatever goods they initially received (both within and across time periods),
and we would have to assume that the absence of any prohibition on such trading
resulted in the successful conclusion of all mutually beneficial transactions.
In other words, the government would have to sanction a "white market" in final
goods rather than confining such operations to a "black market."
2. Alternatively,
the Central Planning Board could create a number of distribution centers to
which people were assigned and distribute some particular quantity of each
final good to each distribution center in each time period.
Assigning
an equal number of people to each center and supplying each center with an equal
portion of each good in each time period, again, is one possibility among many.
In any case, the members of each distribution center could be left to decide how
to distribute whatever goods the center received. But even if we assume that the
distribution among members leaves no possible mutually beneficial transactions
between members, we would have to assume that centers were permitted to trade
their goods (both within and across time periods), and that this trading opportunity
resulted in the conclusion of all mutually beneficial transactions between centers
in order to guarantee Pareto optimality .
Under both these methods of distribution any degree of egalitarianism is theoretically
possible. There are no formal markets in either system. (There is not even any
currency.) But as anyone trained in economics will have recognized, the absence
of markets is something of a sleight of hand. There are no markets only because
all Pareto improvements achievable through exchange are left to individuals to
work out for themselves. It is not difficult to visualize how individual barter
exchange would quickly lead to more and more extensive "classified" sections in
newspapers and eventually monetized markets for final goods. After all, for all
the faults we found with money and markets in chapter 7, we never claimed they
did not serve a practical cybernetic function in particular situations. In a cybernetic
vacuum it is predictable markets would appear. And if the alternative is no information,
or information only at great expense of time and effort, it is reasonable to consider
the emergence of markets a social improvement. In light of which
3. The
Central Planning Board could introduce currency, retail outlets, and savings
and loan banks.
Each individual
could be given some amount of currency in each time period, and all final goods
could be sent to retail outlets. The managers of retail outlets could be directed
to adjust prices to ensure that each good disappeared from the shelf on the last
day of each month, just prior to next month's deliveries. People would freely
loan or borrow from the banks, whose managers would have to finance loans out
of savings deposits, adjusting interest rates to eliminate excess deposits or
loan applications. Provided the retail (and bank) managers perfected the art of
having "empty shelves" just prior to new deliveries, this method would also result
in Pareto optimality . And this holds, of course, without regard to how much currency
each individual is allotted. 4
Obviously, a number of different criteria could be used in deciding how much currency
to give each individual, but the Pareto optimality of central planning would be
preserved under any currency distribution provided we assume the production plan
is carried out. If one were concerned with economic equality
3a. Each
individual could be given the same amount of currency.
On the other hand, if one were concerned that the plan may not be carried out
unless individuals are provided strong material incentives to exert effort in
their work assignments and develop productive skills, other differential currency
disbursements come to mind. For instance:
3b. The
Central Planning Board could give out different amounts of currency to employees
in different production units according to how closely the unit came to fulfilling
its part of the production plan
3c. The
Central Planning Board could distribute different amounts of currency to different
categories of labor depending on how many years of education were required
on average to achieve a certificate of competence in that field
3d. The
Central Planning Board could do studies to rate different jobs according to
relative difficulty and burdensomeness and design pay scales accordingly
3e. The
Central Planning Board could give currency to the personnel departments of
production units with which to hire workers. Workers would freely seek employment
wherever they chose, and personnel departments would freely hire any they
wished from among those who applied. Since this last "criterion" for differential
currency disbursement is also one way of assigning people to jobs, we will
discuss different systems for allocating labor via "free" labor markets next.
9.2.3 Job Assignment
In examining different possible systems of job assignment we should remember that
the Central Planning Board was assumed to have perfect knowledge of the amount
of all different "primary" inputs available-including the number of people capable
of performing each different kind of labor service. Moreover, as part of calculating
an optimal production plan the Central Planning Board calculated the number of
people in each labor category to be assigned to work at each production unit.
What is less obvious is that in calculating an optimal production plan the Central
Planning Board also necessarily calculates the social value (or opportunity cost)
of each scarce input used in producing the optimal production plan, including
each category of labor. In mathematical programming language, those opportunity
costs are called "shadow prices" and are the well-known solutions to the "dual"
programming problem. They are easily (and often automatically) generated along
with the optimal production plan that is the solution to the "primal" programming
problem. This means that the Central Planning Board also knows the opportunity
costs of different categories of labor when they are employed to produce an optimal
production plan.
1. The
simplest method of job assignment would be for the Central Planning Board
to send a letter to each individual in each labor category telling him or
her where to report to work. The Central Planning Board could make the assignments
on any basis they wished-randomly, alphabetically, etc.
2. The
Central Planning Board could leave the specific assignments up to associations
of individuals in each labor category. The Central Planning Board would send
the associations a list of how many of their members should report to each
production unit in the economy and let the associations decide who goes where.
This might be done within any given association by lottery, seniority, or
voting, or with an eye to work and educational incentives. It might be done
according to members' work ratings in their previous employment(s) or their
academic standing in the educational process that qualifies them as members
of the association.
Although the "old" debate did not countenance differential welfare effects of
different work assignments, in fact the situation is theoretically symmetrical
to that of differential welfare effects of different consumption bundles. In this
context, for either of the above systems of job assignments to be Pareto optimal ,
one must assume that all mutually beneficial trades of work assignments between
similarly qualified individuals were both permitted and exhausted before people
showed up to work. But under this assumption of ex post "white markets" within
labor categories, both assignment system I and 2 would satisfy the criterion of
efficiency without resort to formal labor markets.
3. The
Central Planning Board could establish a "free" labor market in the sense
that individual workers would be "free" to search and apply wherever they
chose, and the personnel departments of different units would be "free" to
hire whomever they preferred.
It is important
to realize, however, that such a "free" labor market could operate in three very
different ways.
3a. Under
one system the number of workers hired in each category by each production
unit, as well as the pay rates for each category of worker, would be determined
by the Central Planning Board as part of the overall production plan. The
only decisions left up to individual personnel departments would be which
individuals to hire into positions -and pay rates already determined by the
central plan.
Personnel departments would not be authorized to hire fewer workers of one category
and more of another. Nor would they be authorized to pay wages different from
those set by the Central Planning Board. In other words, production units would
not be permitted to make "input" substitutions or payments differing from nationwide
pay scales which the Central Planning Board could set equal to the labor "shadow
prices" calculated from the optimal production plan. This would be analogous to
the management of a privately owned firm telling its personnel department how
many positions of each kind it was to fill, what wages those individuals would
be paid, and leaving only the hiring of particular employees to the personnel
department.
3b. Alternatively,
the Central Planning Board could allocate to each production unit a wage fund
and leave to the units all decisions about how many workers to hire in each
category and what to pay them.
To determine the size of the wage fund to be given each unit the Central Planning
Board would calculate the number of employees in each category who should work
in that production unit according to the Central Planning Board's optimal production
plan, multiply the number in each category by what the CPB calculated to be the
"shadow price" of that particular scarce labor resource, and deliver the sum total
as the wage fund of the production unit. Then the personnel department of each
production unit could hire whichever individuals in whatever labor categories
it wished, paying them whatever it wished, subject only to the constraint of not
exceeding its total wage fund. This would be analogous to the management of a
private firm giving its personnel department a budget and allowing it to hire
and pay from that budget as it deemed fit.
3c. A
third system is a combination of the first two. The Central Planning Board
would fix the number of employees to be hired in each category in each production
unit, as in the first case. But the personnel departments would have discretionary
powers over wages they contracted to pay particular employees out of a wage
fund that was calculated by the Central Planning Board as in the second case.
This system would be analogous to the management of a private firm determining
how many of each kind of worker to be hired, but allowing the personnel department
to decide who to hire and how much to pay them within an operating budget.
Although the "free" labor market obviously differs in the three different cases,
each has a claim to efficiency under a particular set of assumptions. Under the
assumptions of Model 4, planners are assumed to have perfect knowledge about the
desirabilities of all goods and work activities, the availabilities of all primary
inputs including labor, and the technologies available to all units. Moreover,
the quantities of different categories of labor supplied as well as the effort
exerted are assumed independent of wage rates. Under these assumptions the Central
Planning Board is in a position to calculate optimal allocations of labor as well
as "efficiency" wage rates. But once labor supply is assumed exogenous, not only
is system 3a perfectly efficient with "efficiency" wages, the Central Planning
Board would be free to set wage rates according to any equity criterion without
affecting economic efficiency, 5 permitting
maximum flexibility regarding the degree of equality (or inequality) in the distribution
of labor income.
On the other hand, if the central planners lacked accurate information about the
possibilities of substitution between different labor categories in individual
units, as well as information about differential preferences for different kinds
of work, system 3b would have greater claim to efficiency. But while system 3b
is highly flexible in the sense that it allows maximum room for individual negotiation
for both prospective employees and employers, it would be inflexible regarding
the degree of equality or inequality of labor incomes that could be arranged since
the distribution of labor income would be determined by the forces of supply and
demand. 6
Finally, if the central planners had accurate information concerning labor availabilities
and the production possibility sets of the units, but lacked accurate information
on differential work preferences, system 3c would have greater claims to efficiency.
Before proceeding, we consider a final issue regarding labor assignments totally
ignored in the "old" debate about central planning and efficiency. Whether the
central planners fix hiring quotas and pay rates, allocate wage funds to production
units, or fix hiring quotas but leave pay rates to production unit discretion
within a budget, if the differential desirabilities of work in different units
(units in Siberia versus units in Moscow) are ignored, less attractive units will
have difficulty competing with more attractive units for the better workers within
categories. The "old" debate did not consider differential preferences regarding
work location any more than it did differential preferences for job types. But
once we recognize this issue, it is clear all the above "labor market solutions"
to the job allocation problem of central planning would be subject to inefficiencies
if any such differences were not accounted for. To correct this failing, central
planners would have to enable units that proved only able to hire from the bottom
of the various labor category barrels to pay higher than average wage rates. In
system 3a this would entail authorizing higher pay scales in all categories of
employment in relatively less attractive enterprises. In systems 3b and 3c planners
would have to allocate larger wage funds to less attractive units.
9.2.4 Summary of the "Old Debate"
We hope our treatment of final good distribution and job assignment served to
illustrate the following points:
1. From
the perspective of traditional welfare theory and under the terms of the "old
debate," not only can efficient plans be calculated via central planning,
but the distribution of final goods and job assignments can be carried out
in efficient ways that do not necessarily employ currency, formal markets
for final goods, or formal labor markets.
2. Although
centrally planned systems deemed efficient by traditional welfare theory can,
in theory, operate without markets of any kind, the vision is artificial.
If one accepts traditional welfare theory's view of the possibility of Pareto
improvements through exchange of anything that individuals might value (goods
or jobs), any system of central planning that does not employ markets to distribute
goods or assign people to jobs would quickly generate them or suffer from
distributional inefficiencies.
3. Final
goods markets and labor markets can be part of a centrally planned system
without affecting the mixture of final goods and job roles. The optimal mixtures
can be determined by the central planning procedure with markets used only
for distribution and assignment. 7
4. On
the other hand, final goods and labor markets can be used in a way that allows
them not only to distribute goods and assign jobs that have already been planned,
but to influence the quantities of different final goods and jobs the system
settles on. We defer explaining exactly how this can be done to our discussion
of different ways for determining the relative social values of different
final goods and work activities in the social welfare function. But it is
important to distinguish here between these two very different uses of final
good and labor markets in centrally planned systems.
5. An
improved version of the "old" debate, still from the perspective of traditional
welfare theory, would be to recognize the symmetry between differential preferences
for final goods and differential preferences for different kinds of work by
including different job types and locations, along with final goods, in the
social welfare function.
6. Still,
our major conclusion is that if the central planners are presumed to have
all relevant information, an optimal plan can be calculated, and distribution
and job assignment could be handled in a number of different ways that would
preserve the efficiency of central planning as judged by traditional welfare
theory.
But before leaving the "old" form of the traditional debate to focus on the "modern"
debate concerning information and incentive problems, we consider the efficiency
of central planning under the assumption of endogenous preferences.
9.2.5 The "Old Debate" and Endogenous Preferences
If the Central Planning Board is assumed to know both the developmental as well
as fulfillment effects of economic activity-that is, if the Central Planning Board
knows the true social welfare function-the demonstration that the central planning
can be efficient even under the assumption of endogenous preferences is straightforward.
In this case, the different social evaluations of final goods and labor activities
in the objective function are interpreted to be not only functions of the relative
amounts of different final goods and labor activities consumed in the given time
period, but functions of the relative amounts of different final goods and labor
activities to be consumed in later time periods as well. In this way the future
developmental effects of different production plans would be included in the social
welfare function as well. In other words, in our Model 4 we would want 4.14 to
become:
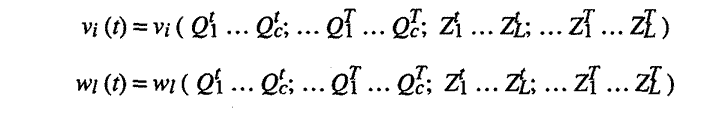
If we extend this further knowledge to the Central Planning Board, the plan they
calculate would obviously be optimal under endogenous preferences, just as when
preferences were assumed exogenous. This completes our review of the "old" debate
about the efficiency of centrally planned economies where informational and incentive
problems are "assumed away." 8
9.3 Round Two: The "Modern Debate"
The planning bureau cannot be aware of all the information needed for a perfect
description of techniques. These are too numerous, complex, and diverse. Only
the individual firms or highly specialized industry offices can have precise knowledge
of the conditions governing production in their particular field. Some way must,
therefore, be found for these firms and offices to participate in the preparation
of the plan. 9
What Malinvaud
means here by "participate" is to provide information to the Central Planning
Board that will allow the Central Planning Board to calculate an optimal production
plan. We now investigate procedures for accomplishing this aim.
10